Серии 31—40 для первого года

31 серия. 7 февраля 2011, пн. Серия про квадраты

1. Геометрия:
   Сколько квадратов можно провести по линиям сетки на рисунке?
       
2. Сколько существует квадратов с вершинами в точках (на другом рисунке)?
3. Нарисуйте на клетчатой бумаге квадрат площадью: а) 2 клетки; б) 5; в) 8; г) 10; д) 13 клеток.
4. В Англии длину измеряют в футах и дюймах. Один фут равен 12 дюймам. А сколько квадратных дюймов в квадратном футе?
5. Арифметика:
   Двузначное число x возвели в квадрат и получили число y. Выяснилось, что если прочесть оба числа задом наперёд, то снова второе будет квадратом первого (но это будут уже другие числа). При этом x не кончается нулём. Найдите хотя бы одно такое x.
6. Придумайте какое-нибудь верное утверждение вида «Если число даёт остаток … при делении на …, то оно не может быть квадратом».
7. Представьте эти числа в виде суммы двух квадратов (пример: 73=8²+3²): 2; 5; 10; 13; 34; 65; 106; 153.
8. Придумайте число, которое нельзя представить в виде суммы: а) двух квадратов; б) трёх квадратов. (Подсказка: это очень просто.)

32 серия. 9—10 февраля 2011, ср—чт. Разрезание

1. Разрежьте каждую из фигур на рисунке на две равные части.
   
   
2. Разрежьте китайский символ «Инь и Ян» одной линией на две равные части так, чтобы каждая его половинка — белая и чёрная — тоже разрезалась на две равные части.
   
   
3. Четырёхугольник разрезали по диагоналям на четыре треугольника. Оказалось, что все четыре треугольника равны. Верно ли, что четырёхугольник был квадратом?
4. Арбуз разрезали на четыре части и съели. Получилось пять корок. Как такое может быть?
5. Шахматную доску разрезали по клеткам на две части. Известно, что в одной части белых клеток вдвое больше, чем чёрных. Верно ли, что в другой части чёрных клеток вдвое больше, чем белых?
6. На клетчатой бумаге нарисовали прямоугольник и закрасили угловые клетки, а потом разрезали на 4 равные части. Может ли оказаться, что закрашенные клетки встречаются ровно в трёх частях из четырёх?

33 серия. 14 февраля 2011, пн

1. На первом листочке выписаны все такие числа от 1 до 100, которые в 7 раз больше суммы своих цифр, а на втором — все числа от 1 до 1000, которые в 70 раз больше суммы своих цифр. На каком листочке чисел больше?
2. Однажды ученики одного класса придумали страшную-страшную игру, в которой не бывает ничьих, и начали в неё играть. Каждый из них сыграл по 15 партий. Обязательно ли найдётся ученик, который одержал: а) хотя бы 8 побед; б) хотя бы 9 побед?
3. В ряд выписаны 10 натуральных чисел, оканчивающихся на разные цифры. После этого первое число увеличивают на 1, второе — на 2, …, десятое — на 10. Докажите, что теперь найдутся два числа, у которых последние цифры совпадают.
4. В красном и зелёном вёдрах есть вода. Если треть воды из красного ведра перелить в зелёное, то в них будет поровну воды. А если вместо этого треть воды из зелёного ведра перелить в красное, то в каком станет больше и во сколько раз?
5. Разрежьте равносторонний треугольник на три треугольника: остроугольный, прямоугольный и тупоугольный.
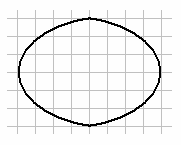
6. С помощью трафарета нарисован овал (см. рисунок). Нарисуйте замкнутую кривую той же длины, которая будет ограничивать площадь на одну клетку больше.
   
   

34 серия. 16—17 февраля 2011, ср—чт

1. Из книги выпал кусок. Первая страница куска имеет номер 387, а номер последней состоит из тех же цифр, но в другом порядке. Сколько страниц в куске?
2. На кружок пришли три мальчика; их имена — Иван, Лёша и Дима, а фамилии — Иванов, Алексеев и Дмитриев. Преподаватель не помнит, кого как зовут. Когда он попросил встать Ивана и Иванова, то встали двое мальчиков, а когда Лёшу и Алексеева, то только один. Установите соответствие между именами и фамилиями.
3. В одном из чёрных углов шахматной доски стоит ферзь, который имеет право ходить только по чёрным клеткам. Может ли он обойти все чёрные клетки доски, побывав в каждой ровно по одному разу, и вернуться в исходную клетку?
4. В запись натурального числа между какими-то двумя цифрами вставляют ноль. Может ли оно от этого увеличиться в 11 раз?
5. Нарисуйте по клеточкам:     а) восьмиугольник с четырьмя сторонами длиной 1 клетка и четырьмя сторонами длиной 2 клетки;     б) двенадцатиугольник с четырьмя сторонами длиной 1 клетка, четырьмя сторонами длиной 2 клетки и четырьмя сторонами длиной 3 клетки.

35 серия. 21 февраля 2011, пн

1. У прямоугольника большую сторону увеличили, а меньшую — настолько же уменьшили. Докажите, что площадь прямоугольника уменьшилась.
2. Квадрат целого числа состоит из 533 цифр. А сколько цифр в самом числе?
3. На плоскости нарисовано 100 точек. Можно ли нарисовать прямоугольник, внутри которого лежат меньше 30 из этих точек, а снаружи — меньше 70? (Считается, что точки на границе прямоугольника не лежат ни внутри, ни снаружи.)
4. На доске 8x8 (клетки не раскрашены) стоят два ферзя. Разрешается разрезать доску а) на две; б) на три; в) на четыре части и, переставив эти части, снова сложить из них доску 8x8. Всегда ли можно добиться того, что ферзи на новой доске будут бить друг друга?
5. Сколько существует чисел от 1 до 1000, у которых произведение цифр равно 13?
6. Прямая покрашена в два цвета (то есть каждая точка прямой покрашена в один из двух цветов). Докажите, что на прямой есть три точки одного цвета, одна из которых лежит точно посредине между двумя другими.

36 серия. 28 февраля 2011, пн

1. В клетках таблицы 3×10 (3 строки, 10 столбцов) расставлены крестики и нолики. Докажите, что какие-то два столбца совпадают.
2. Что больше по площади и насколько: заштрихованная часть фигуры (см. рисунок) или незаштрихованная?
   
   
3. Докажите, что 1·2·…·20 больше, чем 21·22·…·30, но меньше, чем 21·22·…·36.
4. На прямой отмечены точки A, B, C, причём AC:BC=7:4. Чему может равняться AB:AC? Найдите все варианты.
5. Ученики 6«А» класса побывали в музее, в парке и в кино. Учитель попросил оценить их по пятибалльной системе каждое из этих мест. Могут ли одновременно выполняться три утверждения: 1) большинству учеников больше понравилось в музее, чем в парке; 2) большинству учеников больше понравилось в парке, чем в кино; 3) большинству учеников больше понравилось в кино, чем в музее?
6. Можно ли так покрыть всю плоскость квадратами, что среди них будут только два одинаковых?
7. В стране 100 городов, и некоторые из них соединены дорогами. Докажите, что:
8. а) если в стране 98 дорог, то из какого-то города нельзя добраться в какой-то другой город;
9. б) если в стране 100 дорог, то существуют два таких города, что из одного в другой можно добраться хотя бы двумя способами.

37 серия. 2—3 марта 2011, ср—чт

1. Можно ли расставить в клетках таблицы а) 5×5; б) 6×6 целые числа так, чтобы их сумма в каждом столбце была чётной, а в каждой строке — нечётной?
2. Сельский гипнотизёр Иван Карпович разводит индюков и кур. Вследствие его экспериментов десятая часть индюков считает себя курами, а десятая часть кур — индюками. Если считать вместе, пятая часть птиц Ивана Карповича считают себя индюками. А какова доля индюков в его хозяйстве на самом деле?
3. Сторона квадрата на рисунке равна 1. Чему равна закрашенная площадь?
   
   
4. (Эта задача — подсказка к одной из задач предыдущей серии) Что больше: а) 30·42·56·72·90 или 100·85·70·55·40?   б) 100·85·70·55·40 или 5·6·6·7·7·8·8·9·9·10?
5. Анечка выписала те из чисел от 1 до 700, которые не делятся на 7. Докажите, что сумма Аниных чисел делится на 7.
6. Каждый день на стадионе «Гадюкино» проходил упорный футбольный матч – всякий раз он заканчивался победой одной из команд  с перевесом в один мяч. Могло ли за неделю быть наколочено 50 голов?
7. 16 команд премьер-лиги сыграли каждая с каждой по матчу. Восемь команд одержали по 8 побед и по 6 раз сыграли вничью, еще семь команд одержали по 2 победы и по 5 раз сыграли вничью. Сколько ничьих у 16-й команды?

38 серия. 9—10 марта 2011, ср—чт

1. Поставьте на доске несколько коней так, чтобы каждый бил ровно двух других. Какое минимальное количество коней для этого нужно?
2. Можно ли на доске а) 8×8; б) 80×80 поставить ферзей, не бьющих друг друга, так, чтобы они держали под боем всю доску? Считаем, что ферзь бьёт клетку, на которой стоит.
3. Бабушка оставила козу пастись на поле: вбила два колышка на расстоянии 10 метров, натянула между ними верёвку, на верёвку надела кольцо, к кольцу привязала поводок длиной 5 метров, а к поводку, наконец, прицепила козу. Вернувшись, бабушка увидела вокруг колышков участок без травы. Нарисуйте этот участок (можно в уменьшенном масштабе). Размерами козы пренебречь.
4. На доске 8×8 закрашены некоторые клетки, причём в любом прямоугольнике площадью больше 8 закрашено чётное количество клеток. Может ли такое быть?
5. Факториалом натурального числа n называют произведение n!=1·2·…·(n-1)·n. Что больше: 100! или 1!+2!+3!+…+99! ?

39 серия. 14 марта 2011, пн

1. Ребята решили подарить 12 девочкам цветы на восьмое марта. Они купили им тюльпаны (всем по равному нечётному количеству). Но на поздравление пришло только 8 девочек. Докажите, что: (а) ребята теперь не смогут раздарить девочкам тюльпаны, подарив каждой по одинаковому нечётному количеству; (б) но если разрешить дарить девочкам разное нечётное количество тюльпанов, то можно раздарить все.
2. Друг напротив друга стоят два вражеских войска — «жёлтые» и «синие», в каждом по 100 воинов. В некий момент все жёлтые стреляют в синих. Через минуту все выжившие синие стреляют в жёлтых. Известно, что каждый воин либо промахивается, либо убивает (сразу же) одного противника. Какое наибольшее число воинов может быть убито после того, как каждое войско выстрелит по разу?
3. Придумайте какую-нибудь сумму денег, которую можно заплатить одной монетой, можно двумя, можно тремя, а можно — четырьмя.
4. У детей есть по одной карточке с изображением собаки, волка, медведя и зайца. Они вставляют эти карточки на место пропусков в рассказ охотника: «Однажды я с ..... охотился на ..... . Вдруг я увидел на снегу следы ..... . В испуге я помчался прочь, но зверь был быстрее. Впрочем, когда он меня настиг, оказалось, что это был всего лишь .....». Сколько разных рассказов (не обязательно правдоподобных) может получиться у детей?
5. Аня пишет в тетради все буквосочетания, которые можно получить перестановкой букв в слове САЛАТ (включая и исходное слово). Боря делает то же самое для слов: а) АТЛАС; б) ХАЛАТ; в) САЛЮТ. У кого из них получится больше слов и во сколько раз?
6. Дано два одинаковых квадрата. Разрежьте каждый из них на две части и из этих частей сложите один квадрат.

40 серия. 16—17 марта 2011, ср—чт

1. Существует ли натуральное число, большее единицы, которое не делится ни на одно из чисел от двух до тысячи?
2. Можно ли разрезать доску 10×10 на L-тетрамино?
3. У нумизмата Феди есть монеты диаметром не больше 10 см, которые лежат в коробке 30×70 см (в один слой). Феде подарили монету диаметром 25 см. Докажите, что теперь все монеты поместятся в коробку 55×55 см.
4. Найдите девять таких последовательных целых чисел, что сумма шести первых равна сумме трех последних.
5. На заседании по делу об украденной муке Мартовский Заяц заявил, что вор — Болванщик. Болванщик и Соня тоже дали показания, которые, однако, не были записаны. Позже выяснилось, что муку украл лишь один из троих, и лишь он дал правдивые показания. Кто украл муку?
6. Двое братьев работают в одной фирме. Каждый день за хорошую работу каждый брат получает 7 тугриков, за плохую — 3. За несколько дней один из братьев получил (а) 21 тугрик; (б) 19 тугриков. Какое наибольшее и наименьшее количество тугриков мог получить за то же время второй брат?
7. 16 шестиклассников играют в шашки. Докажите, что в любой момент найдутся два шестиклассника, сыгравшие к этому моменту одинаковое количество матчей.